반응형
| 보낸사람 | 
| belle |
| 받는사람 | 고강사 | |||||
| 날짜 | 2007. 9. 28 오후 8:11 | |||||
|
저 시험도 안보고 그냥 precal/cal됐어요 정말 황당ㅋㅋㅋㅋㅋ 휴,,,,, 일단 지금 인터넷이 잘 안되기 때문에 되는 시간을 이용해서 어서 질문 부터 할게요 f(x)=2sin2x-3cos2x 를 f(x)=a sin (b(x-h)) 꼴로 바꾸래요 이런식의 질문이 계속나오는데 삼각함수 식을 합성하는 뭐 그런 종류 같은데 몰르겠어요 막 코사인하고 사인하고 합친 식의 그래프를 그리라그러고 ㄷㄷㄷㄷㄷㄷㄷ 정말 굴욕입니다 우리 클래스에 9학년 저 혼자... 나머지 10학년 11학년 심지어 12학년도 있어요 그러고 한국 사람이 반이상이에요 그나마 지금 선배언니한테 그래프 그릴때 계산기 이용법을 다시 배우고 정신을 찾고 있어요.. 그럼 저는 이만 수업이 있어서 가볼게요.. 감사합니다~~~~!^^ |
---------------------------------------------------------------------------------------
| 보낸사람 | 고강사 |
| 받는사람 | 
| belle | ||||
| 날짜 | 2007. 9. 28 오후 9:03 | |||||
| 제목 | Re: 쌤 | |||||
유학생'ㅈ'. 거기는 몇시입니까??
이 메일을 받은 것이 8시11분(물론 오후)이고 9시에 답장을 쓰니 거의 실시간?!?!
질문하신 내용은 삼각함수의 합성에 관련된 부분입니다.
기본은 이렇습니다.
sin(A+x) =sinAcosx+cosAsinx <= 삼각함수 덧셈공식은 기본이고, 배웠기 때문에 기억이 나야하오!!!
그런데, 합성의 경우에는 이렇습니다.
1/2 cosx + √3/2 sinx = ?
자, 이 경우에 sin이 1/2이고, cos이 √3/2 인 각도가 있습니다. 몇 도일까요~?
정답은 30˚ 입니다. 따라서 위 식은 다음처럼 생각할 수 있습니다.
1/2 x cosx + √3/2 sinx = sin30˚cosx + cos30˚sinx = sin(30˚+x)
아하~ 감이 오십니까? 와야되는데.... ㅡ_ㅡ
그럼 이번에는
f(x)=2sin2x-3cos2x 을 봅시다. <= 정양이 적어준 식
아놔~ 큰일입니다. 왜냐하면 sin이 2이고 cos이 -3인 각도가 대체 어딨냐 말입죠~
그래서 다음처럼 식을 바꿉니다. (크기가 1을 넘지 않도록 하기 위해서...)
f(x)= 2sin2x -3cos2x = √2^2+(-3)^2 { 2 / √2^2+(-3)^2 sin2x + (-3) / √2^2+(-3)^2 cos2x }
= √2^2+(-3)^2 { (-3) / √2^2+(-3)^2 cos2x + 2 / √2^2+(-3)^2
sin2x} (그냥 앞뒤 순서 바꾼것임)
(빨간 부분은 보기가 힘든데 루트 (2의제곱+(-3)의제곱) 입니다.
이식은 그냥 원점으로부터 (2,-3)까지의 거리, 또는 벡터 (2,-3)의 크기)
이렇게 묶어주면 sin,cos앞에 곱해지는 숫자가 항상 1보다 작거나 같아집니다.
(당연하지 크기로 나눴는데...)
그러면 늘 하던대로 4사분면을 그리시고, 반지름이 √2^2+(-3)^2 원을 생각하면
sin과 cos이 각각 (-3) / √2^2+(-3)^2, 2 / √2^2+(-3)^2 인 각도를 생각할 수 있습니다.
지금은 보아하니, sin이 'ㅡ' 이고 cos이 '+' 니까 4사분면의 각입니다.
이것을 θ(270˚<θ<360˚) 라고 합시다.
(늘 하던 얘기대로 30˚, 45˚, 60˚에 해당하는 경우가 아니면 알 수 없으니 그냥 θ로 표시)
그러면 다시 주어진 식으로 돌아가서
f(x) = 2sin2x -3cos2x = √2^2+(-3)^2 { 2 / √2^2+(-3)^2 sin2x + (-3) / √2^2+(-3)^2 cos2x }
= √2^2+(-3)^2 { (-3) / √2^2+(-3)^2 cos2x + 2 / √2^2+(-3)^2
sin2x}
= √2^2+(-3)^2 { sinθcos2x + cosθsin2x }
= √2^2+(-3)^2 sin (θ+2x)
입니다. 오케바리 입니까?!?!
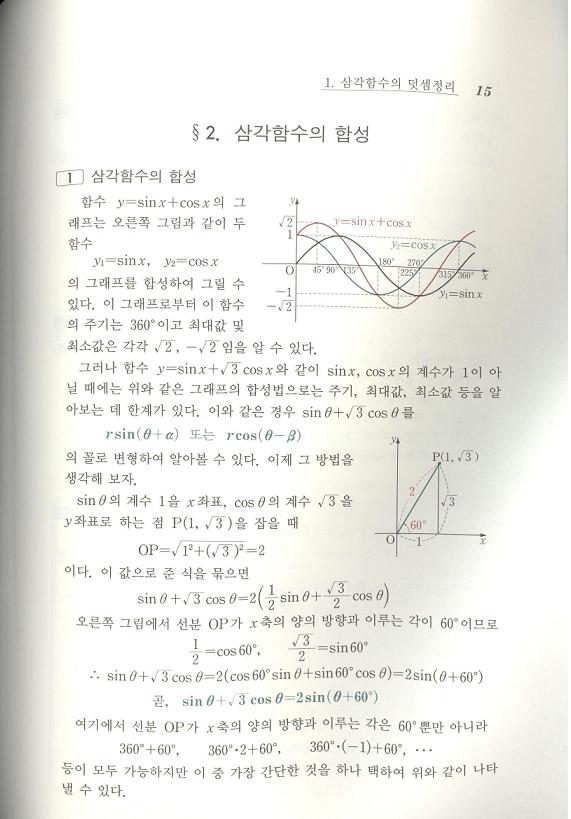
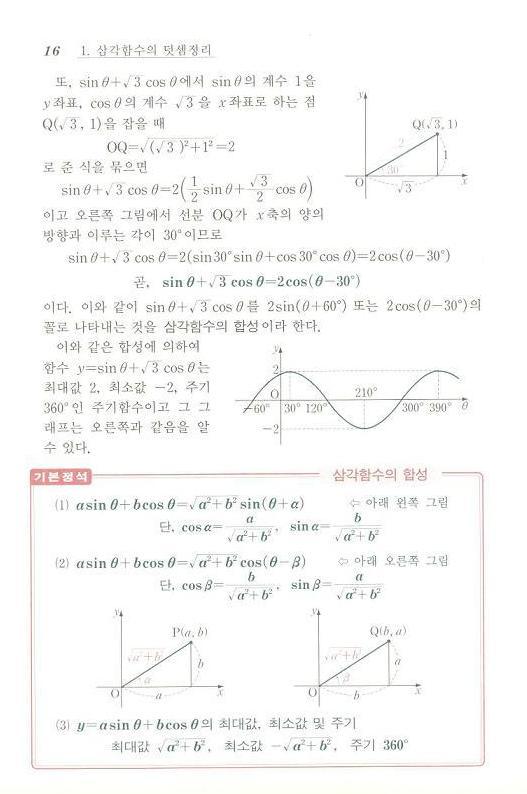
첨부한 정석그림에 딱딱한 설명이 나와 있고, 보기문제가 3문제 정도 있으니 풀어보시압~
그리고도 모르겠으면 또! 질문!! 답답하면 화상채팅도 가능 ( 부끄~)
언제라도 질문하시고, 굴욕을 넘어서 9학년 천재 수학소녀가 되시길... 홧팅!
p.s 한글이나 워드가 있으면 한글이나 워드문서로 첨부하는게 편하겠소만...
다음 질문에서는 한글이나 워드 보유여부 (version 반드시 명시!!) 알려주시오.




012
반응형
'Q&A' 카테고리의 다른 글
| [Q] 극좌표로 표현된 두 점 사이의 거리 (0) | 2009.05.21 |
|---|---|
| TI-89 Titanium 에서 산점도(Scatter Plot) 그리는 법 (0) | 2009.03.16 |
| Q&A 게시판 신설 (0) | 2007.07.29 |